| Orthogonal projections in B6 Coxeter plane | |||
|---|---|---|---|
 7-orthoplex |
 Pentellated 7-orthoplex |
 Pentitruncated 7-orthoplex |
 Penticantellated 7-orthoplex |
 Penticantitruncated 7-orthoplex |
 Pentiruncinated 7-orthoplex |
 Pentiruncitruncated 7-orthoplex |
 Pentiruncicantellated 7-orthoplex |
 Pentiruncicantitruncated 7-orthoplex |
 Pentistericated 7-orthoplex |
 Pentisteritruncated 7-orthoplex |
 Pentistericantellated 7-orthoplex |
 Pentistericantitruncated 7-orthoplex |
 Pentisteriruncinated 7-orthoplex |
 Pentisteriruncitruncated 7-orthoplex |
 Pentisteriruncicantellated 7-orthoplex |
 Pentisteriruncicantitruncated 7-orthoplex | |||
In seven-dimensional geometry, a pentellated 7-orthoplex is a convex uniform 7-polytope with 5th order truncations (pentellation) of the regular 7-orthoplex.
There are 32 unique pentellations of the 7-orthoplex with permutations of truncations, cantellations, runcinations, and sterications. 16 are more simply constructed relative to the 7-cube.
These polytopes are a part of a set of 127 uniform 7-polytopes with B7 symmetry.
Pentellated 7-orthoplex
| Pentellated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 20160 |
| Vertices | 2688 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Small terated hecatonicosoctaexon (acronym: Staz) (Jonathan Bowers)[1]
Coordinates
Coordinates are permutations of (0,1,1,1,1,1,2)√2
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentitruncated 7-orthoplex
| pentitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 87360 |
| Vertices | 13440 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Teritruncated hecatonicosoctaexon (acronym: Tetaz) (Jonathan Bowers)[2]
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Coordinates
Coordinates are permutations of (0,1,1,1,1,2,3).
Penticantellated 7-orthoplex
| Penticantellated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 188160 |
| Vertices | 26880 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Terirhombated hecatonicosoctaexon (acronym: Teroz) (Jonathan Bowers)[3]
Coordinates
Coordinates are permutations of (0,1,1,1,2,2,3)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Penticantitruncated 7-orthoplex
| penticantitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 295680 |
| Vertices | 53760 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Terigreatorhombated hecatonicosoctaexon (acronym: Tograz) (Jonathan Bowers)[4]
Coordinates
Coordinates are permutations of (0,1,1,1,2,3,4)√2.
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentiruncinated 7-orthoplex
| pentiruncinated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,3,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 174720 |
| Vertices | 26880 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Teriprismated hecatonicosoctaexon (acronym: Topaz) (Jonathan Bowers)[5]
Coordinates
The coordinates are permutations of (0,1,1,2,2,2,3)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentiruncitruncated 7-orthoplex
| pentiruncitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 443520 |
| Vertices | 80640 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Teriprismatotruncated hecatonicosoctaexon (acronym: Toptaz) (Jonathan Bowers)[6]
Coordinates
Coordinates are permutations of (0,1,1,2,2,3,4)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentiruncicantellated 7-orthoplex
| pentiruncicantellated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,3,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 403200 |
| Vertices | 80640 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Teriprismatorhombated hecatonicosoctaexon (acronym: Toparz) (Jonathan Bowers)[7]
Coordinates
Coordinates are permutations of (0,1,1,2,3,3,4)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentiruncicantitruncated 7-orthoplex
| pentiruncicantitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 725760 |
| Vertices | 161280 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Terigreatoprismated hecatonicosoctaexon (acronym: Tegopaz) (Jonathan Bowers)[8]
Coordinates
Coordinates are permutations of (0,1,1,2,3,4,5)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph | too complex |  |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentistericated 7-orthoplex
| pentistericated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 67200 |
| Vertices | 13440 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Tericellated hecatonicosoctaexon (acronym: Tocaz) (Jonathan Bowers)[9]
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Coordinates
Coordinates are permutations of (0,1,2,2,2,2,3)√2.
Pentisteritruncated 7-orthoplex
| pentisteritruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 241920 |
| Vertices | 53760 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Tericellitruncated hecatonicosoctaexon (acronym: Tacotaz) (Jonathan Bowers)[10]
Coordinates
Coordinates are permutations of (0,1,2,2,2,3,4)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentistericantellated 7-orthoplex
| pentistericantellated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 403200 |
| Vertices | 80640 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Tericellirhombated hecatonicosoctaexon (acronym: Tocarz) (Jonathan Bowers)[11]
Coordinates
Coordinates are permutations of (0,1,2,2,3,3,4)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentistericantitruncated 7-orthoplex
| pentistericantitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 645120 |
| Vertices | 161280 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Tericelligreatorhombated hecatonicosoctaexon (acronym: Tecagraz) (Jonathan Bowers)[12]
Coordinates
Coordinates are permutations of (0,1,2,2,3,4,5)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph | too complex |  |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentisteriruncinated 7-orthoplex
| Pentisteriruncinated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,3,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 241920 |
| Vertices | 53760 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Bipenticantitruncated 7-orthoplex as t1,2,3,6{35,4}
- Tericelliprismated hecatonicosoctaexon (acronym: Tecpaz) (Jonathan Bowers)[13]
Coordinates
Coordinates are permutations of (0,1,2,3,3,3,4)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentisteriruncitruncated 7-orthoplex
| pentisteriruncitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 645120 |
| Vertices | 161280 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Tericelliprismatotruncated hecatonicosoctaexon (acronym: Tecpotaz) (Jonathan Bowers)[14]
Coordinates
Coordinates are permutations of (0,1,2,3,3,4,5)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph | too complex |  |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentisteriruncicantellated 7-orthoplex
| pentisteriruncicantellated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,3,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 645120 |
| Vertices | 161280 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Bipentiruncicantitruncated 7-orthoplex as t1,2,3,4,6{35,4}
- Tericelliprismatorhombated hecatonicosoctaexon (acronym: Tacparez) (Jonathan Bowers)[15]
Coordinates
Coordinates are permutations of (0,1,2,3,4,4,5)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph | too complex |  |
 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Pentisteriruncicantitruncated 7-orthoplex
| pentisteriruncicantitruncated 7-orthoplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,4,5{35,4} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 1128960 |
| Vertices | 322560 |
| Vertex figure | |
| Coxeter groups | B7, [4,35] |
| Properties | convex |
Alternate names
- Great terated hecatonicosoctaexon (acronym: Gotaz) (Jonathan Bowers)[16]
Coordinates
Coordinates are permutations of (0,1,2,3,4,5,6)√2.
Images
| Coxeter plane | B7 / A6 | B6 / D7 | B5 / D6 / A4 |
|---|---|---|---|
| Graph | too complex |  |
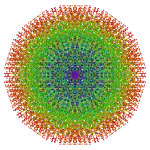 |
| Dihedral symmetry | [14] | [12] | [10] |
| Coxeter plane | B4 / D5 | B3 / D4 / A2 | B2 / D3 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry | [6] | [4] |
Notes
- ↑ Klitzing, (x3o3o3o3o3x4o - )
- ↑ Klitzing, (x3x3o3o3o3x4o - )
- ↑ Klitzing, (x3o3x3o3o3x4o - )
- ↑ Klitzing, (x3x3x3oxo3x4o - )
- ↑ Klitzing, (x3o3o3x3o3x4o - )
- ↑ Klitzing, (x3x3o3x3o3x4o - )
- ↑ Klitzing, (x3o3x3x3o3x4o - )
- ↑ Klitzing, (x3x3x3x3o3x4o - )
- ↑ Klitzing, (x3o3o3o3x3x4o - )
- ↑ Klitzing, (x3x3o3o3x3x4o - )
- ↑ Klitzing, (x3o3x3o3x3x4o - )
- ↑ Klitzing, (x3x3x3o3x3x4o - )
- ↑ Klitzing, (x3o3o3x3x3x4o - )
- ↑ Klitzing, (x3x3o3x3x3x4o - )
- ↑ Klitzing, (x3o3x3x3x3x4o - )
- ↑ Klitzing, (x3x3x3x3x3x4o - )
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "7D uniform polytopes (polyexa)".